这篇文章最初被发表在Medium上。

一个区块中的交易总量是一个重要的信息。我们将展示如何在没有可信任的第三方的情况下来获取它，这一行为在以前被认为是不可能的。

范围

我们将默克尔路径的长度表示为n。叶节点的数量，即在一个区块中的交易数量，是介于2^(n-1) + 1到2^n之间的。您要了解这一点，一个高度为n的完美二叉树¹，有2^n个叶结点。默克尔路径的长度与默克尔树的高度相同。

[caption id="attachment_474000" align="alignnone" width="700"]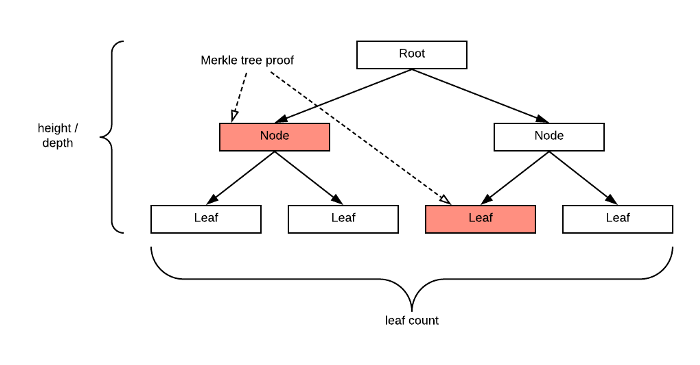 一个高度为2的完美树[/caption]

确切的数量

找到最后一笔交易

在上一篇文章中，我们已经访问了区块中的第一笔coinbase交易。如果我们也可以访问最后一笔交易，我们就能够推断出交易的总数。我们可以通过验证其默克尔路径上的所有节点都在右侧分支来确定第一笔/最左侧的交易。通过要求所有默克尔路径的节点都位于左侧分支，就很容易以类似的方式找到最后/最右侧的交易。很不幸的是，这可能并不总是正确无误的。

如果我们有一个完美的默克尔树，那么在最后一笔交易中的默克尔路径上的所有节点实际上都在左侧的分支上，如下图所示。

[caption id="attachment_474003" align="alignnone" width="700"]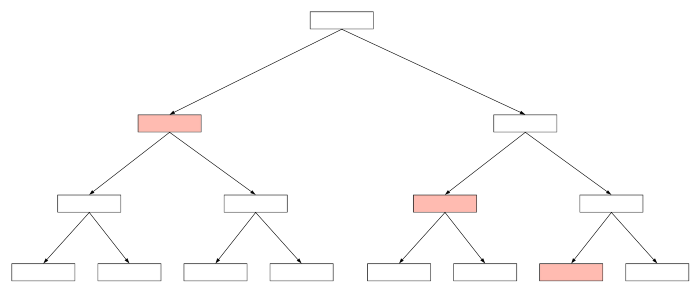 彩色标出的部分都是最后一笔交易的默克尔路径[/caption]

然而，当树不处于完美情况的时候，情况就变得不一样了。例如，下面的树共有5个叶节点，最后一笔交易的默克尔路径由所有的橙色节点所组成。其中的两个节点在右侧的分支上，只有最上面的一个节点在左侧分支上。

[caption id="attachment_474006" align="alignnone" width="700"]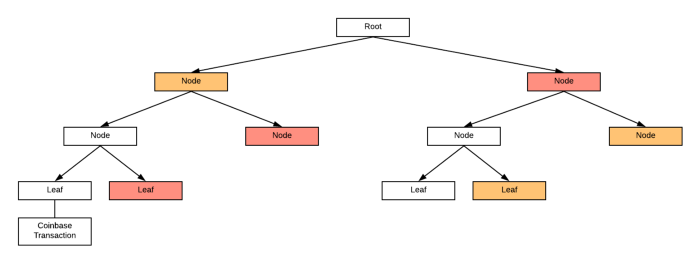 第一笔和最后一笔交易的默克尔路径分别都被用红色与橙色标记出来了[/caption]

为了克服这个问题，我们注意到，当默克尔树的任何一层中存在奇数个节点时，最后一个节点将重复出现上面出现的内容。这意味着，如果最后一笔交易的默克尔路径上的任何节点位于右侧的分支，则它一定是从当前的左侧分枝上复制下来的，如下图所示。

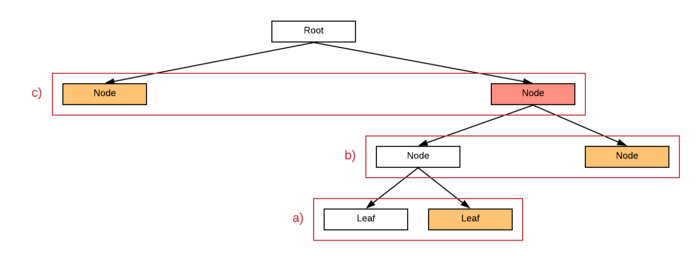
以下的代码能够直接实现这种算法。

[caption id="attachment_474015" align="alignnone" width="1358"]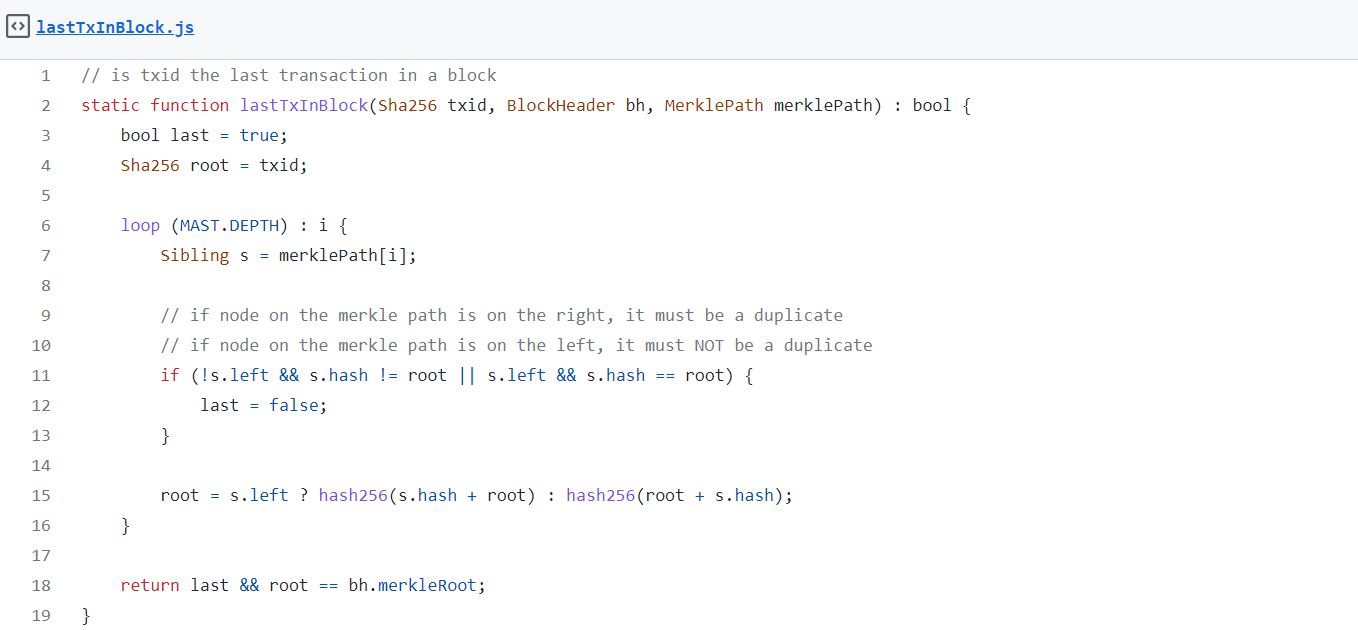 区块链合约[/caption]

从默克尔之路到交易索引

为了获得交易的索引，我们沿着它的默克尔路径从根到代表它的叶节点。当路径上的一个节点位于左分支时，我们就向右进（即二进制1）；否则，我们向左进（二进制0）。我们可以清晰地看到，通过这种方式我们能够得到它用二进制表现出来的索引。在下面的例子中，我们把这个规则应用到最后一笔交易上，然后我们一直往右就得到了二进制的111，这也正是它的十进制索引7。

[caption id="attachment_474018" align="alignnone" width="700"] 一个所有叶节点索引都是二进制形式的树[/caption]

这个代码如下所示：

[caption id="attachment_474020" align="alignnone" width="1369"]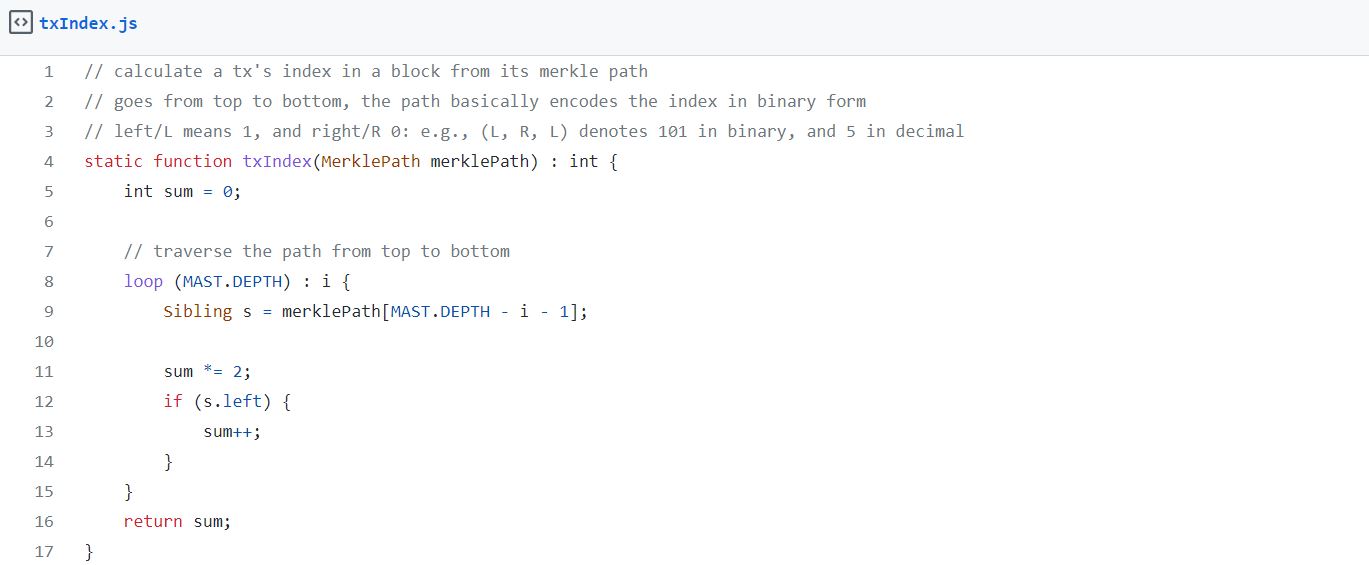 区块链合约[/caption]

得出确切的交易计数

最后，我们可以将这两个函数组合成blockTxCount()，它将确切的交易数量发回到区块中。

[caption id="attachment_474022" align="alignnone" width="1358"]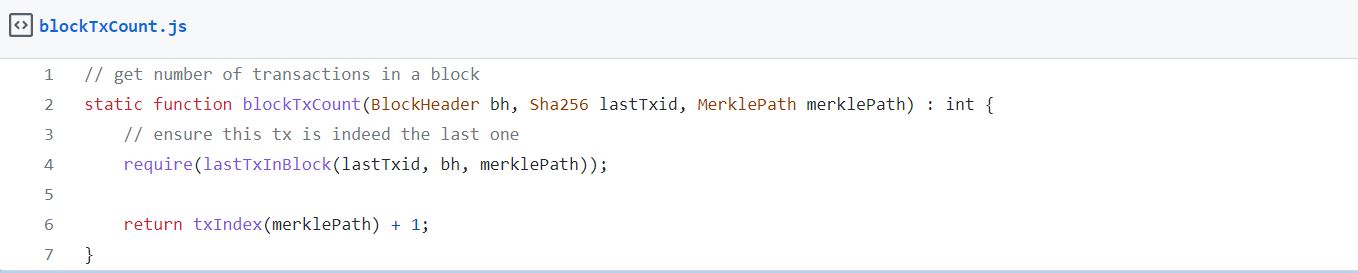 区块链合约[/caption]

总结

一旦我们可以访问一个区块中的交易数量，那么我们就可以用它来构建以前被认为是不可能实现的智能合约。下面我们只列举几个例子：

• 当一个区块包含超过100万笔交易时，我们可以通过签订一份赏金协议来赞助压力测试。
• 结合之前获得的时间信息，无论是在区块头中的时间戳还是区块高度，每秒交易量（TPS）都可以被准确无误地计算出来并且在合约中使用。例如，只有在TPS达到10万时才会解锁的合约。

我们期待看到你们能提出什么样的令人兴奋的新合约。

鸣谢

这篇文章的灵感来自于shilch的工作成果。

另请观看：CoinGeek纽约大会小组讨论，使用区块链获得的更好互联网体验